字符串匹配算法
文章目录
本文记录字符串匹配算法的演进已经具体实现。
字符串匹配算法(String Search Algorigthm)
一点说明:
原串:即子串匹配过程中, 待查找的字符串;
搜索串:即用来匹配的特定的一个子串。
1 KMP算法 (The Knuth-Morris-Pratt Algorithm)
优点:在暴力解法的基础上,减少匹配过程中查找字符串比较次数。
缺点:当待查找的字符串没有重复搜索串时,算法退化为暴力解法。
算法中的概念:
局部匹配表(partial match table):查找过程中的子串中真前缀和真后缀的最大公共长度。
字符串的真前缀(proper prefix):例如 “S”, “Sn”, “Sna”, 和 “Snap” 都是 “Snape”的proper prefix。
字符串的真后缀(proper suffix):例如“d”,“agrid”, “grid”, “rid”, “id”和 都是“Hagrid”的proper suffix。
计算局部匹配表(partial math table)
局部匹配表有时也称为next数组。该表是由子串的内容决定的。计算过程如下(以下过程以字符串"abababca"为例):
-
字符串长度为1时,字符串为"a"。因此对应表项为0。
-
字符串长度为2时,字符串为“ab”,proper prefix包含“a”;proper suffix包含“b”,因此对应表项为0。
-
字符串长度为3时,字符串为“aba”,proper prefix包含“a”, “ab”; proper suffix包含“a”,“ba”,因此对应表项为1。
-
字符串长度为4时,字符串为“abab”,proper prefix包含“a”, “ab”,“aba”;proper suffix包含“b”,“ab”,“bab”,因此对应表项为2。
-
字符串长度为5时,字符串为“ababa”,proper prefix包含“a”, “ab”,“aba”,“abab”;proper suffix包含“a”,“ba”,“aba”,“baba”,因此对应表项为3。
-
字符串长度为6时,字符串为“ababab”,proper prefix包含“a”, “ab”,“aba”,“abab”,“ababa”;proper suffix包含“b”,“ab”,“bab”,“abab”,,因此对应表项为3。

使用局部匹配表进行字符串匹配
设局部匹配表为table。如果存在部分匹配值partial_match_length,而且table[partial_match_length] > 1,则子串可以跳过的长度为:partial_match_length - table[partial_match_length - 1] 。例如:
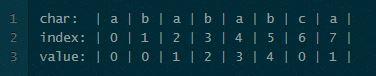
第一次匹配情况,如下图所示:

该匹配中部分匹配长度(partial_match_length)为1。而对应的值table[partial_match_length - 1]即table[0]等于0。因此我们不需要跳过任何字母。 接下来的匹配情况如下图所示:

该匹配中部分匹配长度为(partial_match_length)为5。这个值对应的table[partial_match_length - 1](即table[4])值为3。这意味着partial_match_length - table[partial_match_length - 1](即5 - talbe[4],即5-3,即2)。即子串向右移动2个字符。如图所示:

移动后的匹配情况如上图所示,匹配成功长度(partial_match_length)为3。对应的table[partial_match_length - 1](即table[2])值为1。意味着我们向后移动长度为:partial_match_length - table[partial_match_length - 1](即3 - table[2] = 3 - 1 = 2)。移动后的结果如图所示:

因子串尾部以超过原串长度,因此结束匹配。
2 BM算法 (Boyer-Moore Algorithm)
1977年,德克萨斯大学的Robert S. Boyer教授和J Strother Moore教授发明了这种算法。因此取这两个人的名字而得。word中的查找功能就是使用该算法。
算法中的概念:
- 坏字符(bad character):字符串匹配过程中,与搜索串不匹配的字符。
- 好后缀(good suffix): 即搜索串与原串尾部能够匹配的字符串。
坏字符实例,如下图:



好后缀实例,如下图:

比较规则:首先,将搜索串与原串对齐,从搜索串尾部从后往前比较。
坏字符移动规则: 后移位数 = 坏字符的位置 - 搜索词中的上一次出现位置。说明,若搜索串中不包含坏字符,则搜索串上一次出现位置为-1。若包含该字符,则为离坏字符位置最近的那个位置。
好后缀规则 :后移位数 = 好后缀的位置 - 搜索词中的上一次出现位置。好后缀位置以后缀最后一个位置为准。说明,若搜索串中不包含坏字符,则搜索串上一次出现位置为-1。例如:
- 如果字符串"ABCDAB"的后一个"AB"是"好后缀"。那么它的位置是5(从0开始计算,取最后的"B"的值),在"搜索词中的上一次出现位置"是1(第一个"B"的位置),所以后移 5 - 1 = 4位,前一个"AB"移到后一个"AB"的位置。
- 如果字符串"ABCDEF"的"EF"是好后缀,则"EF"的位置是5 ,上一次出现的位置是 -1(即未出现),所以后移 5 - (-1) = 6位,即整个字符串移到"F"的后一位。
注意:
- 以上两个规则的中的位置指的是搜索串中的位置。
- 当通过坏字符规则和好后缀移动规则得到的值不同时,取较大的值作为移动量。
下面以字符串为"HERE IS A SIMPLE EXAMPLE",搜索词为"EXAMPLE"为例,进行说明:
step1:
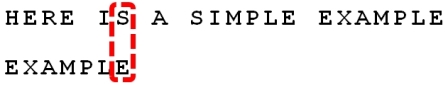
首先遇到坏字符,计算移动位置:6 - (-1) = 7. step2:

遇到坏字符,计算移动位置:6 - 4 = 2.
step3:

遇到好后缀,计算移动位置:6 - 0 = 6。
step4:
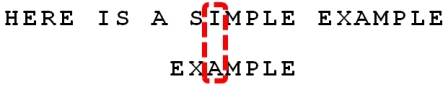
坏字符和好后缀的选择问题:
坏字符的结果:
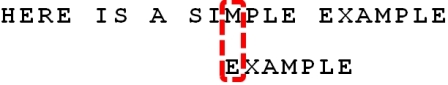
后后缀的结果:
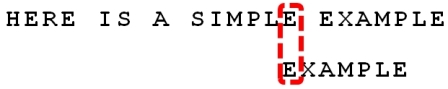
step5:
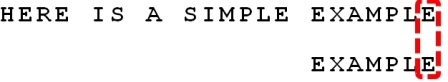
3 Sunday算法(Sunday Algorigthm)
sunday算法是对BM算法的改进。改进之处:当匹配失败时,判断搜索串下次匹配位置的第一个字符是否与搜索串第一个字符是否相同。进而减少匹配次数。